Sinus, cosinus og tangens
Vi vil her beskæftige os med tre grundlæggende trigonometriske funktioner: Sinus, cosinus og tangens.
Disse tre funktioner har det tilfælles at hvis vi fodrer dem med en vinkel, så giver de et magisk tal tilbage. Der er altså inden i disse funktioner noget magi og nogle nisser som laver en vinkel om til et tal!

I de næste par afsnit vil vi forsøge at forstå sammenhængen mellem den vinkel vi fodrer funktionen med og det tal nisserne leverer. På den måde kan vi måske komme nærmere på hvorfor Sin(), Cos() og Tan() er så seje som alle matematikere synes.
Enhedscirklen
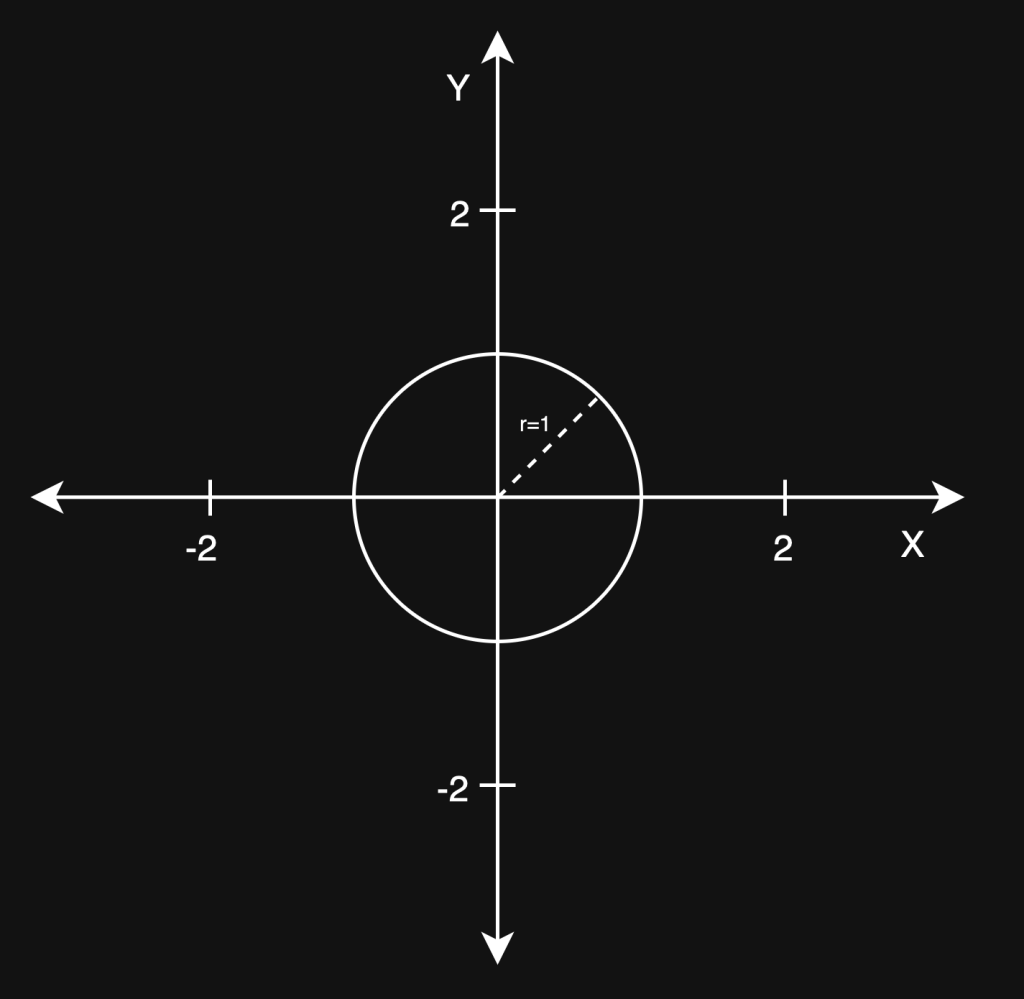
Det geometriske værktøj vi vil benytte for at forstå hvorledes de trigonometriske funktioner fungerer kaldes enhedscirklen. Enhedscirklen lever både i det kartesiske samt det komplekse plan, og er en cirkel der er så heldig at den har centrum i Origo og dens radius er tallet 1.
Den version vi vil beskæftige os med her er den kartesiske enhedscirkel og den ser således ud:
Sinus & cosinus
Selvom mange matematikundervisere mere eller mindre frivilligt gør sinus og cosinus til en gåde er deres funktion simpel. De tager en vinkel som input og leverer et tal som output. Det viser sig at det tal de leverer afhænger af enhedscirklen som illustreret på fig. 3.
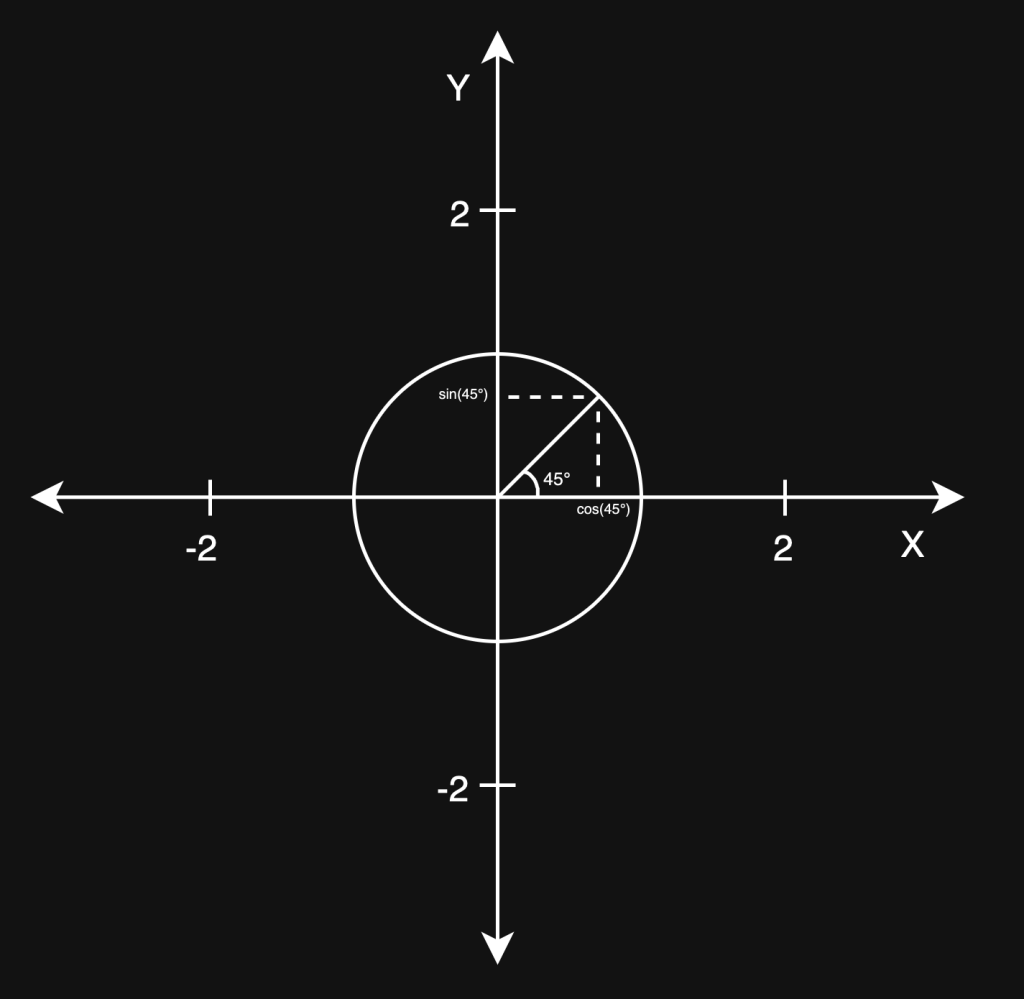
Ved inspektion af figur 3, erfarer man at sinus og cosinus blot fortæller os hvor vi er på enhedscirklen givet en vinkel. Giver vi foreks. både sinus og cosinus vinklen 45 grader, returnerer de et punkt på enhedscirklen. I tilfældet hvor vinklen er 45 grader findes dette punkt:
$P[sin(45), cos(45)] = P(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$
Tangens
Nu skulle man tro at når sinus og cosinus opfører sig så pænt at de altid returnere en værdi med relation til et punkt på enhedscirklen, så burde deres fætter tangens opføre sig lige pænt. Men ikke helt, tangens er nemlig en værre bandit der skyder helt forbi målet så at sige. Hvordan dette hænger sammen ses på figuren.
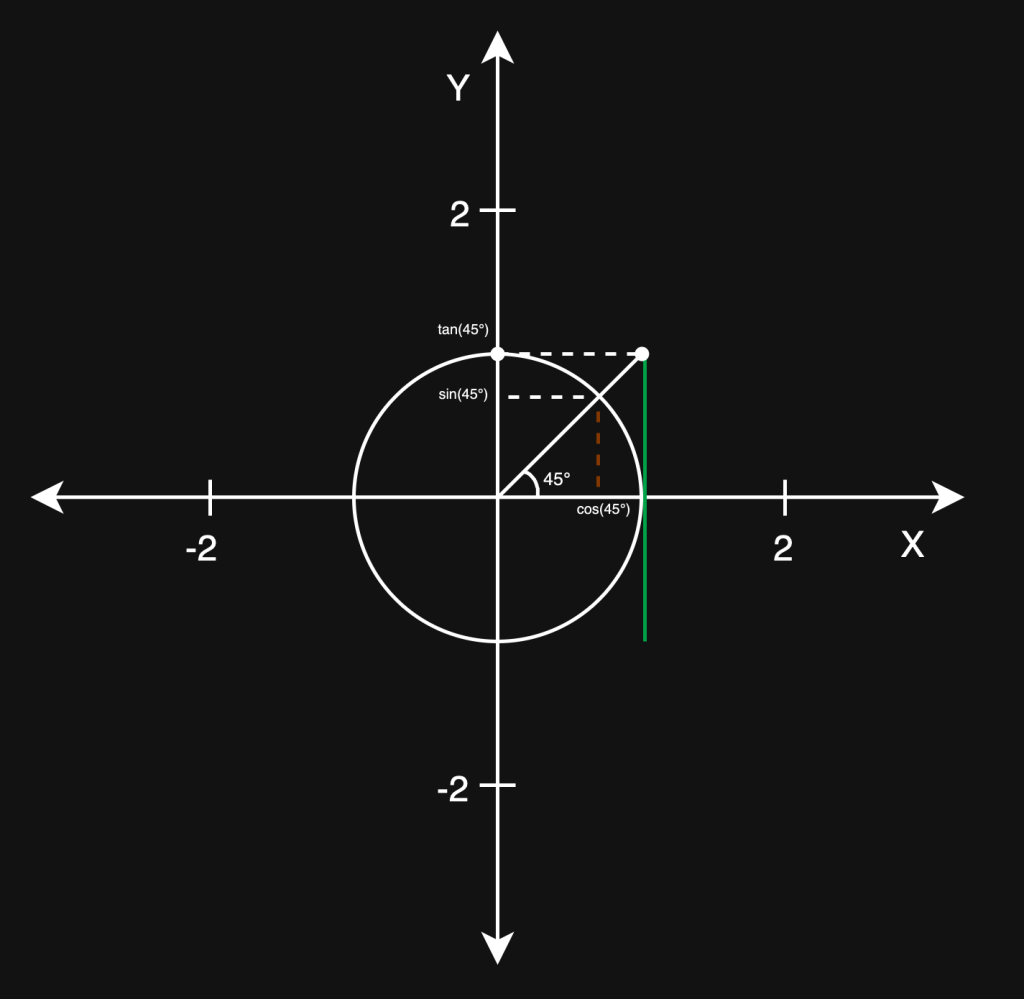
Der ses at output af tangens er nedfældningen på y-aksen af det punkt der opstår når to specifikke linjer skæres. De to linjer er på figuren henholdsvis en forlængelse af den samme linje som skærer enhedscirklens omkreds, og den linje(grøn) der tangerer cirklen.
Hvis man nu er lidt snedig og betragter figuren nøje, vil man opdage at der fremkommer to ensvinklede trekanter. Den ene trekants højde er markeret med brun og den andens højde er det stykke af den grønne linje der strækker sig fra x-aksen og op til skæringspunktet. Da forholdet mellem kateterne i to ensvinklede trekanter er ens og den store trekants grundlinjes absolutte værdi altid er tallet 1, kan vi altså nu sige:
$ \frac{\sin(v)}{\cos(v)} = \frac{\tan(v)}{|1|} = \tan(v)$
Hvilket tilfældigvis også er definitionen på tangens. Du har nu lært hvorledes sinus, cosinus og tangens hænger sammen og måske også indset at det ikke er magiske, uforklarlige funktioner.
Universet imploderer og alt liv bliver udryddet hvis…
Den ualmindeligt opmærksomme læser vil have bemærket at der opstår en uheldig situation hvis vi fodrer tangens med vinklerne 90 og 270 grader. Hvis vi skal følge vores tidligere definition af tangens vil vi nemlig komme frem til følgende:
$ \frac{|\sin(90)|}{\cos(90)} = \frac{|\sin(270)|}{\cos(270)} = \frac{1}{0} = UNDEFINED $
Da der er umuligt at dele en lagkage i nul dele, har vi altså nu indset at tangens til 90 og 270 grader ikke er defineret.
Hvis du har nogle kommentarer eller spørgsmål til denne artikel er du meget velkommen til at skrive en besked herunder.